What's that?
Remember those lessons of statistics you had long ago? Factorial?
Combination? Well, we'll take those formulas to show how you can
develop a mobile application using various SDK's and tools.
Factorial
Let's say we have letters A, B and C. How many "words"
can we make, using each letter only once. By word, we mean "any
series of three letters, even if it's not in a dictionary".
ACB is one of them. Let's list all of'em: ABC, ACB, BAC, BCA, CAB,
CBA. Another way to look at it is to say:
- For the first letter, I can pick A, B or C, which means I have
3 possibilities. Let me pick A.
- Then, for the second letter, I can only pick B or C, which means
2 possibilities. I pick B
- Finally, the only option left for the last letter is C: 1 possilibity
The total number of words is 6: three possibilities multiplied
by two possibilities then by one. Hey that works! Look at our enumeration
of words a bit above! Great... We just illustrated how to calculate
a factorial: factorial(3)=3x2x1=6. You'll write this as 3! =
6.
4! = 4x3x2x1 = 4 x (3x2x1)= 4 x 3!
5! = 5x4x3x2x1 = 5 x (4x3x2x1) = 5 x 4!
1000! = 1000x999x998x997x...x1 = 1000 x 999!, or as a general definition:
n! = n x (n-1)!
Combination
Now, let's take another example. You would like to win the prize
of this $1000 lottery. Here's the rule: there are five balls numbered
1 thru 5 and you must pick two of them. How many combinations are
there? Well, go back to our previous example and apply the same
principle here:
- For the first ball, I have 5 choices
- For the second one, I only have 4 choices
- For the third one... Hey, wait a minute, there is NO such "third
one". You are allowed to pick only two numbers!
The total number of choices is 5 x 4 = 20.
Really? Is is THAT simple? Well, not quite! Let's see why. Here's
a list of all the combinations:
- 1 2
- 1 3
- 1 4
- 1 5
- 2 1... Er... Really?!? No
way!!! Actually, in any lottery, "1 and 2" is
same as "2 and 1"
- 2 3... This one is okay, let's continue on without repeating
choices as in previous bullet
- 2 4
- 2 5
- 3 4
- 3 5
- 4 5
In other words, ORDER doesn't count. Well, it's a good thing for
us whenever we buy a lottery ticket, as this gives us the chance
to win if the winner is "ball 5 and ball 2" and we chose
"ball 5 and ball 2".
So, we'll have to divide our "5 x 4 = 20" from above
by 2. If we had to pick 3 balls, we would divide 5 x 4 x 3 by 3
x 2, because there are 3x2 ways of making a "three-letter word
out of three given letters".
You will notice that 5 x 4 = (5 x 4 x 3 x 2 x 1) / (3 x 2 x 1)
= 5! / 3!
The final result is 5! / 3! / 2! = 10. Check this formula against
the list above.
You probably know that 3 = 5 - 2.
Remember? 5 is the total number of balls and 2 is how many of'em
we can pick. The general formula to calculate the number of combinations
of n items taken by p at a time is:
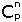= n! / (n-p)! / p! = n! / [(n-p)! x p!]
Our sample
This small app implements three modules:
- factorial
- combination, which calls factorial three times, as the formula
states
- go, which calls factorial(n), factorial(p), factorial(n-p) just
to display intermediate values, and finally combination(n, p)
I intentionally didn't optimize this application. In a commercial
app, it would make sense to not code the combination formula as
is. It'd be smarter to calculate a "partial factorial"
than to calculate two factorials and divide them.
Same remark for recursion. We did use recursion whenever the language's
implementation allowed it. Again, a simple loop would run quicker
and save stack space, which is very valuable on our small devices
:)
|
